|
A consumer's preferences can be represented by a utility function if they satisfy properties P.1 through P.4, and one additional property called continuity. Continuity is probably the least intuitive property of preferences, yet it is not implausible.
|
|
Preferences are continuous if the set of all choices that are at least as good as a choice x' and the set of all choices that are no better than x' are both closed sets. In the notation of sets, this is written as {x : x 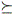 x'} and {x : x' x'} and {x : x' 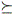 x} are both closed. x} are both closed.
|
|
One definition of a closed set is that any sequence of points in the set that converges, converges to a point of the set. In this context, that means that for a sequence of points {xn} with n = 1, 2, 3, ..., if x 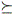 xn for every xn and if xn converges to some consumption point x', then x xn for every xn and if xn converges to some consumption point x', then x 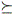 x'. x'.
Figure 6 shows an example of this. In the figure, if x 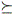 xn for every n, and if xn converges to x', then continuity implies that x xn for every n, and if xn converges to x', then continuity implies that x 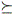 x'. x'.
|
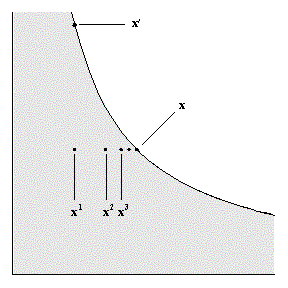
Figure 6: Sequence of points xn that converge to x'.
|
|
If a consumer has a preference relation 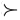 that
is complete, reflexive, transitive, strongly monotonic, and continuous, then these preferences can be represented by a continuous utility function u(x) such that
u(x) > u(x') if and only if x that
is complete, reflexive, transitive, strongly monotonic, and continuous, then these preferences can be represented by a continuous utility function u(x) such that
u(x) > u(x') if and only if x 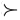 x'. x'.
|
|
Proof : Let e = (1, 1, ..., 1). For each x, define u(x) by u(x) e 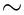 x. Then u(x) is a utility function for the preferences x. Then u(x) is a utility function for the preferences 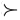 if if
1. such a function u(x) exists,
2. the function u(x) is unique, and
3. u(x) > u(x') if and only if x 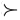 x'. x'.
|
|
Let B = {a: a e 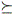 x}. If x = (x1, x2), let y = (max{x1, x2}, max{x1, x2}). Then strong monotonicity implies that y x}. If x = (x1, x2), let y = (max{x1, x2}, max{x1, x2}). Then strong monotonicity implies that y 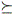 x, so B is not empty.
Let W = {a: x x, so B is not empty.
Let W = {a: x 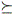 a e}. Then 0 is an element of W, so W is not empty. By completeness, B a e}. Then 0 is an element of W, so W is not empty. By completeness, B 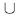 W = {a : a W = {a : a 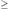 0}. Both B and W are closed sets, from property P.5 (continuity), so B 0}. Both B and W are closed sets, from property P.5 (continuity), so B 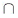 W is not empty. Therefore, there is some a such that a e W is not empty. Therefore, there is some a such that a e 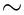 x. By strong monotonicity, if a' > a, then a' e x. By strong monotonicity, if a' > a, then a' e 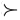 x, and if a' < a, then x x, and if a' < a, then x  a' e, so a is unique. Let u(x) = a. So u(x) exists and it is unique. a' e, so a is unique. Let u(x) = a. So u(x) exists and it is unique.
Next, we want to show that u(x) represents the preferences  . Suppose that x and y are two consumption levels and u(x) = ax where a x e . Suppose that x and y are two consumption levels and u(x) = ax where a x e 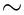 x. Let u(y) = a y where a y e x. Let u(y) = a y where a y e 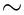 y. If a x > a y then by monotonicty a x e y. If a x > a y then by monotonicty a x e  a y e. By transitivity, x a y e. By transitivity, x  a x e a x e  a y e a y e  y. Finally, if x y. Finally, if x  y, then a x e y, then a x e  a y e so that a x > a y. a y e so that a x > a y.
|