|
|
|
|
A consumer's preferences can be represented by a utility function if they satisfy properties P.1 through P.4, and one additional property called continuity. Continuity is probably the least intuitive property of preferences, yet it is not implausible. |
|
P.5 The "Continuity" Property |
|
Preferences are continuous if the set of all choices that are at least as good as a choice x' and the set of all choices that are no better than x' are both closed sets. In the notation of sets, this is written as {x : x |
|
One definition of a closed set is that any sequence of points in the set that converges, converges to a point of the set. In this context, that means that for a sequence of points {xn} with n = 1, 2, 3, ..., if x |
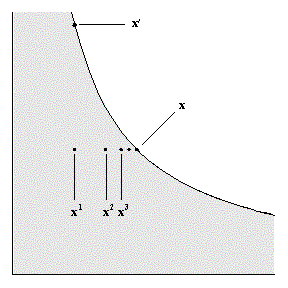 Figure 6: Sequence of points xn that converge to x'. |
|
Representation Theorem |
|
If a consumer has a preference relation |
|
Proof : Let e = (1, 1, ..., 1). For each x, define u(x) by u(x) e |
|
Let B = {a: a e |
|
|
Page source: http://www.econport.org/econport/request?page=man_consumer_choice_preferences_representation
|