|
|
|
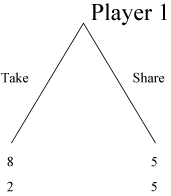
Punishment-MUG Dictator Control 1 is a dictator game in which player 1 chooses between Take and Share and player 2 has no decision to make. Player 1 does not have to be afraid of any possible punishment by the other player and can thus choose his preferred outcome.
|
|
The Punishment-MUG Dictator Control 1 eliminates the possible motive of fear of negative reciprocity that might be present in player 1?s behavior when playing the original Punishment-MUG game.
|
- There are 2 players participating in the game: player 1 and player 2.
- $10 is to be divided between them.
- Player 1 decides whether to Share and propose an equal split of ($5, $5) or Take i.e. propose an unequal split of ($8, $2).
- Player 2 has no decision to make ? the proposed split is implemented.
|
|
|
The unique Nash prediction for player 1 with selfish preferences is to choose ?Take? since it leads to higher monetary payoffs.
|
|
The comparison of players? 1 decisions in the punishment-MUG game and the decisions in the Punishment Dictator Control 1 discriminates between choices of Share that are motivated by fear of negative reciprocity and choices that are motivated by non-reciprocal other-regarding preferences.
|
|
In Cox and Deck [2002] 64% of players 1 chose Take in the original Punishment-MUG game and 70% chose Take in PDC1. This means that more participants of the experiment decided to chose the unequal decision when the paired player 2 did not have a chance to punish them than when this opportunity existed. From comparison of data one can conclude that first movers? behavior in the Punishment-MUG game is not characterized by fear of negative reciprocity.
|
|
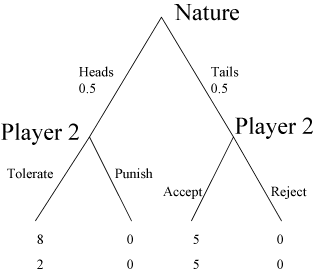
Punishment-MUG Dictator Control 2 is a dictator game in which player 1 does not make a decision. The choice is determined by a random process when the strategies Take and Share can be selected with an equal probability. Since the situation player 2 is in was not chosen by player 1, player 2 has no reason to punish him. Thus the difference between player 2?s decision in the punishment-MUG game and Punishment Dictator Control 2 game discriminates between player 2?s choices of ($0, $0) outcome motivated by negative reciprocity and choices motivated by non-reciprocal inequality-averse preferences.
|
|
The Punishment-MUG Dictator Control 2 eliminates the possible motive of negative reciprocity that might be present in players? behavior when playing the original Punishment-MUG game.
|
- There are 2 players participating in the two-stage game: player 1 and player 2.
- $10 is to be divided between them.
- Player 1 has no decision to make
- Stage 1: Nature decides with a probability of ½ whether player 2 will find himself in the ?Share node? of the game tree corresponding to an equal split of ($5, $5) or in the ?Take node? corresponding to an unequal split of ($8, $2) when both outcomes are equally likely to occur (both with a probability of ½.)
- Stage 2: before making his/her move player 2 knows the outcome of stage 1.
- If in the ?Share node? of the game tree, player 2 can either Accept what results in payoffs ($5, $5) or Reject ($0, $0).
- If in the ?Take node,? player 2 can choose to either Tolerate ($8, $2) or Punish ($0, $0).
|
|
|
Player 2 with self-regarding preferences prefers the strategies Tolerate to Punish when in the ?Take node? and Accept to Reject when in the ?Share node?.
|
|
Let?s again look at Cox and Deck [2002] results. After being offered an unequal split only 21% of players 2 chose punish. This behavior can be described as negative reciprocity only if it is the case that players 2 prefer the outcome ($8, $2) to ($0, $0) when players 1 have not made any decision that would harm players 2. Only 3 out of 13 (23%) players 2 in PCD2 who hade to decide whether to Tolerate or Punish because of the outcome of the coin flip chose Punish. The difference in the behavior of players 2 in the Punishment-MUG game and PCD2 does not support the evidence of negative reciprocity in this experiment what is consistent with the expectations of players 1.
|
- Cox, James C. and Cary Deck, ''On the Nature of Reciprocal Motives,'' University of Arizona discussion paper, 2002.
- Cox, James C. and Daniel Friedman, "A Tractable Model of Reciprocity and Fairness," University of Arizona discussion paper, September 2002.
- Falk, Armin, Ernst Fehr, and Urs Fischbacher, ?On the Nature of Fair Behavior,? Economic Inquiry, forthcoming.
- Hoffman, Elizabeth, Kevin A. McCabe, Keith Shachat, and Vernon L. Smith, ?Preferences, Property Rights, and Anonymity in Bargaining Games,? Games and Economic Behavior, VII(1994), pp. 346-80.
|
| |