Students / Subjects

Handbook >> Consumer Demand and Revealed Preference >> Choices and Preferences >>

Representation of Preferences by a Utility Function

A consumer's preferences can be represented by a utility function if they satisfy properties P.1 through P.4, and one additional property called continuity. Continuity is probably the least intuitive property of preferences, yet it is not implausible.

P.5 The "Continuity" Property

Preferences are continuous if the set of all choices that are at least as good as a choice x' and the set of all choices that are no better than x' are both closed sets. In the notation of sets, this is written as {x : x is at least as good as x'} and {x : x' is at least as good as x} are both closed.

One definition of a closed set is that any sequence of points in the set that converges, converges to a point of the set. In this context, that means that for a sequence of points {xn} with n = 1, 2, 3, ..., if x is at least as good as xn for every xn and if xn converges to some consumption point x', then x is at least as good as x'.

Figure 6 shows an example of this. In the figure, if x is at least as good as xn for every n, and if xn converges to x', then continuity implies that x is at least as good as x'.


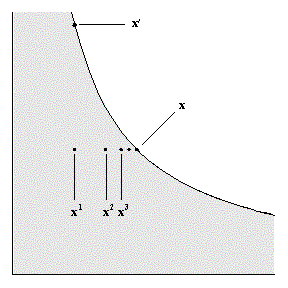
Figure 6: Sequence of points xn that converge to x'.

Representation Theorem

If a consumer has a preference relation is at least as good as that is complete, reflexive, transitive, strongly monotonic, and continuous, then these preferences can be represented by a continuous utility function u(x) such that u(x) > u(x') if and only if x is at least as good as x'.

Proof : Let e = (1, 1, ..., 1). For each x, define u(x) by u(x) e is indifferent to x. Then u(x) is a utility function for the preferences is preferred to if
1. such a function u(x) exists,
2. the function u(x) is unique, and
3. u(x) > u(x') if and only if x is at least as good as x'.

Let B = {a: a e is at least as good as x}. If x = (x1, x2), let y = (max{x1, x2}, max{x1, x2}). Then strong monotonicity implies that y is at least as good as x, so B is not empty. Let W = {a: x is at least as good as a e}. Then 0 is an element of W, so W is not empty. By completeness, B union W = {a : a is greater than or equal to 0}. Both B and W are closed sets, from property P.5 (continuity), so B intersection W is not empty. Therefore, there is some a such that a e is indifferent to x. By strong monotonicity, if a' > a, then a' e is preferred to x, and if a' < a, then x is preferred to a' e, so a is unique. Let u(x) = a. So u(x) exists and it is unique.

Next, we want to show that u(x) represents the preferences is at least as good as. Suppose that x and y are two consumption levels and u(x) = ax where a x e is indifferent to x. Let u(y) = a y where a y e is indifferent to y. If a x > a y then by monotonicty a x e is preferred to a y e. By transitivity, x is indifferent to a x e is preferred to a y e is indifferent to y. Finally, if x is preferred to y, then a x e is preferred to a y e so that a x > a y.

Next

Copyright 2006 Experimental Economics Center. All rights reserved. Send us feedback