|
|
|
|
One objective of the models of choice is to evaluate how choices change as the set of alternative choices change. Demand relates observed choices to the price level for a commodity. Price changes are one form of change to the set of available alternative choices. So the first problem that we need to address is how to represent the set of alternative choices that are available to a consumer. |
|
The Consumption Space |
|
One of the most common problems in consumer choice is the choice of a consumption level for each of a number of commodities, each with a fixed price, when income is fixed. It is not too difficult to formulate and analyze this type of problem even when the number of commodities is large, but the problem is greatly simplified and the ideas can be described graphically when there are only two commodities, so we begin the description of the consumer choice model for that case. If the consumption levels for commodities 1 and 2 are x1 |
|
Limited income and positive prices for each of the
two commodities produces a finite set of alternative choices, which is often called a |
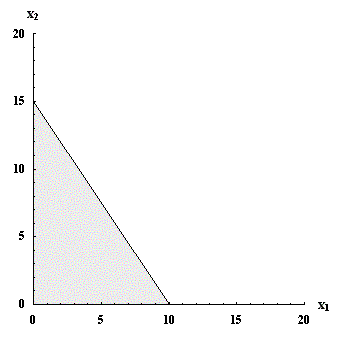 Figure 1: Budget set with prices p1 = 12, p2 = 8, and income M = 120. Next |
|
|
Page source: http://www.econport.org/econport/request?page=man_consumer_budget
|