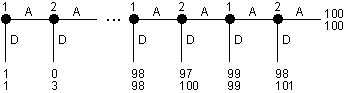
The picture above depicts a popular game known as the centipede game. The centipede game was popularised by Rosenthal(1981).

The way to solve this game is to apply backwards induction. If we see look at the next to final node player 2 will surely choose D, taking 101 instead of 100 and leaving player 1 with 98 instead of 100. this is because playing A is dominated by playing D for player 2. So, at the next to final node player 1 will choose D, taking 99 instead of the 98 he would have got by choosing A and letting 2 choose D. This will leave player 2 with 99 and so he in turn a node earlier will chosse D and take 100. And so on- going back up the tree, players 1 and 2 always take D instead of A, winding up with 1 choosing D at the first node in the game for a payoffs of 1 for each player, whereas each player would receive 100 if they played to the end of the tree.

However, based on experimental evidence this is not the best prediction of actual reality, and asked to play the game, one typically finds even the more sophisticated players moving a fair ways out towards the end before one of them chooses D. For a discussion of experiments using the centipede game click here