|
|
|
|
Investment Game |
|
The investment game is a sequential game with salient fairness considerations. In its structure it incorporates many motives of behavior present in everyday life, such as altruistic or inequality-averse other-regarding preferences and trust in positive reciprocity.
|
|
Game Rules |
|
The investment game is played by two players, both endowed with $10. The game has two stages. In stage 1 the first mover decides how much money to pass to an anonymous second mover. All money passed is increased by a multiplicative factor greater than 1, for example 3. In stage 2 the second mover then decides how much to return to the first mover. |
|
Overview of the Most Common Setup: |
|
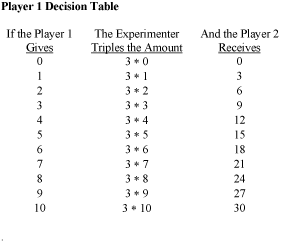
|

|
|
Nash Prediction for the Self-Regarding Preferences Model |
|
The unique subgame perfect Nash prediction for the self-regarding preferences model with perfect information is to pass zero money, since a self-interested person would return nothing in the final stage. It can be solved for by using the backward induction method. This subgame perfect Nash equilibrium is Pareto-inferior to some alternative feasible allocations when player 1 passes a positive amount of money to player 2 which increases the stake to be divided between them. First movers are commonly observed passing money to second movers. Thus, explanations of this behavior have incorporated alternative motives for behavior, including trust, reciprocity, and fairness. |
|
Common Experimental Results |
|
It has been often observed that players 1 identify the possibility of creating a surplus by sending positive amounts to paired players 2 and use trust for mutual gain. For example, in the Berg, Dickhaut, and McCabe (1995) experiment 55 out of 60 players 1 send at least some money. These amounts were then tripled by the experimenters and thus resulted in higher total payoffs to the players. Furthermore, many players 2 returned various amounts of money to players 1. |
|
Possible Explanations of Non-Selfish Behavior |
|
|
|
To test for quantitative effects of altruistic or inequality-averse other-regarding preferences, trust in positive reciprocity, and positive reciprocity itself, one can use a triadic design incorporating dictator controls. For the descriptions of Investment Game Dictator Controls see the Dictator Game section. |
|
Example of Trusting and Reciprocal Behavior in the Investment Game: |
|
A first mover gives the maximum amount of money, i.e. $10, to the second mover; thus the allocation after stage 1 is ($0, $40). The second mover can decide to reciprocate the behavior and give part or all $40 to the first mover; let this amount be x. Thus the first and second movers are left with an allocation ($x, $40-x) after stage 2. If x>= $10 then the final allocation is Pareto superior to the endowments ($10,$10). |
|
Available Experiments |
|
|
|
Further Readings |
|
|
|
|
Page source: http://www.econport.org/econport/request?page=man_tfr_experiments_invgame
|